Noise Generators
Generating Stationary Sensor Signals in Isotropic Noise Fields
Researchers in the signal processing community often require sensor signals that result from a spherically or cylindrically isotropic noise field for simulation purposes. Although it has been shown that these signals can be generated using a number of uncorrelated noise sources that are uniformly spaced on a sphere or cylinder, this method is seldom used in practice. In [1] we proposed different algorithms to generate sensor signals for an arbitrary one- and three-dimensional array that result from a spherically or cylindrically isotropic noise field. Furthermore, the influence of the number of noise sources on the accuracy of the generated sensor signals is investigated. The details of the algorithms are described in [1] and [2].
The latest MATLAB implementation can be downloaded here.
Generating Nonstationary Sensor Signals Under a Spatial Coherence Constraint
Noise fields encountered in real-life scenarios can often be approximated as spherical or cylindrical noise fields. The characteristics of the noise field can be described by a spatial coherence function. For simulation purposes, researchers in the signal processing community often require sensor signals that exhibit a specific spatial coherence function. In addition, they often require a specific type of noise such as temporally correlated noise, babble speech that comprises a mixture of mutually independent speech fragments, or factory noise. Existing algorithms are unable to generate sensor signals such as babble speech and factory noise observed in an arbitrary noise field. In [3] an efficient algorithm is proposed that generates multisensor signals under a predefined spatial coherence constraint. The benefit of the developed algorithm is twofold. Firstly, there are no restrictions on the spatial coherence function. Secondly, to generate M sensor signals the algorithm requires only M mutually independent noise signals. The performance evaluation shows that the developed algorithm is able to generate a more accurate spatial coherence between the generated sensor signals compared to the so-called image method that is frequently used in the signal processing community.
The latest MATLAB implementation can be downloaded here.
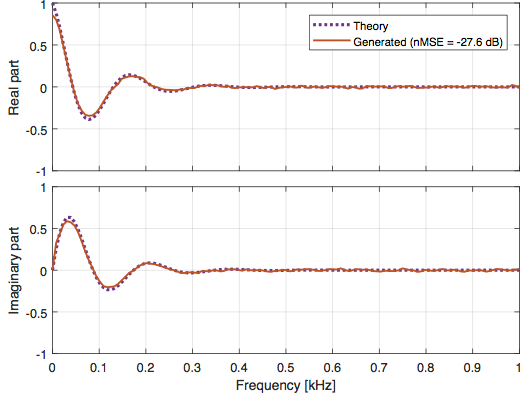
Generating Multi-Channel Wind Noise
For the development and performance evaluation of wind noise reduction algorithms, a controlled environment is required: a large variety of wind noise samples must be added to clean speech samples with a predefined input SNR to measure the achieved noise suppression. The challenging task of wind noise capturing motivates the design of synthetically generated signals; outdoor measurements are often disrupted by diverse acoustic sources (e.g., traffic, natural ambient sounds etc.) from which pure wind noise is difficult to isolate. The artificial generation overcomes the time-consuming challenge of collecting pure wind noise samples for noise reduction evaluations and provides flexibility in the number of generated signals used in the simulations. The developed algorithm is able to generate multi-channel artificial wind noise signals exhibiting a complex coherence given by a fluid-dynamics model, namely the Corcos model. The latter is defined in the discrete-frequency domain using the microphone axis as reference system. Following the model, the complex coherence of wind noise signals depends on the inter-microphone distance, the direction of the air stream and the free-field flow velocity. In particular, the source-filter model in [4] is extended to generate N uncorrelated wind noise signals under defined assumptions on the shared temporal and spectral characteristics. The subsequent complex coherence constraint is achieved using the algorithm presented in [3]. The performance evaluation shows that the complex coherence of synthetically generated wind noise signals closely match the theoretical model. More details about the Corcos model, its validation through experimental data and the algorithm to generation multi-channel wind noise can be found in [5]. An audio example can be found here.
The latest MATLAB implementation can be downloaded here.
References
-
E.A.P. Habets and S. Gannot
Generating sensor signals in isotropic noise fields, Journal of the Acoustical Society of America, Vol. 122, Issue 6, pp. 3464-3470, Dec. 2007. -
E.A.P. Habets and S. Gannot
Comments on `Generating sensor signals in isotropic noise fields', internal report, Sept. 2010. -
E.A.P. Habets, I. Cohen and S. Gannot
Generating nonstationary multisensor signals under a spatial coherence constraint, Journal of the Acoustical Society of America, Vol. 124, Issue 5, pp. 2911-2917, Nov. 2008. -
C. M. Nelke and P. Vary, “Measurement, analysis and simulation of wind noise signals for mobile communication devices,” in the Proc. pf the International Workshop on Acoustic Signal Enhancement (IWAENC), pp. 327–331, 2014.
-
D. Mirabilii and E.A.P. Habets, "Simulating multi-channel wind noise based on the Corcos model," in the Proc. Intl. Workshop Acoust. Signal Enhancement (IWAENC): 560–564, 2018.

