Following Section 5.1.1 of [Müller, FMP, Springer 2015], we introduce in this notebook some basic facts on musical intervals.
Introduction¶
In music, an interval may be loosely defined as the difference between two pitches. This definition is problematic in the sense that the underlying notion of pitch is already a rather vague one. As we discussed in the FMP notebook on musical notes and pitches, pitch is a perceptual property that allows the ordering of sounds on a frequency-related logarithmic scale. When playing a note of a certain pitch on an instrument, the resulting musical tone is dominated by certain frequencies referred to as partials. The frequency of the lowest partial is called the fundamental frequency, which is the frequency typically associated to the pitch. For harmonic sounds, the partials are (close to) integer multiples, the harmonics, of the fundamental frequency. The most basic interval in music is the octave, which is defined as the distance between a pitch and another one with half or double its fundamental frequency. Starting with this basic interval, one can define notions of other intervals by considering frequency relations of harmonics (physical approach), geometric relations (mathematical approach), or note relations (musical approach). These approaches lead to slightly different notions of intervals, which are however referred to by the same interval names. In this notebook, we will discuss some of these notions and the resulting inconsistencies.
Semitone Differences¶
Assuming a twelve-tone equal-tempered scale, an octave is subdivided into twelve scale steps that are equally spaced on a logarithmic frequency axis. The smallest possible interval in this scale is called a semitone, which is the difference between two subsequent scale steps. In terms of frequencies, a semitone describes a ratio (rather than a difference), which can be specified using the logarithmic unit of cents. Recall that the difference in cents between two frequencies, say $\omega_1$ and $\omega_2$, is given by
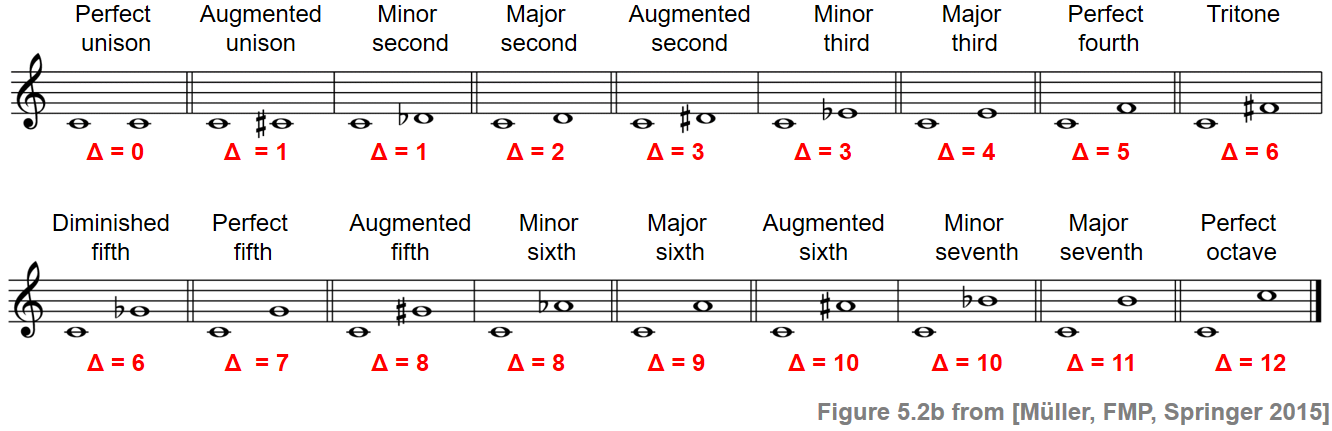
\begin{equation} \log_2\left(\frac{\omega_1}{\omega_2}\right)\cdot 1200. \end{equation}Thus, in the equal-tempered scale, a semitone corresponds to $100$ cents. Based on the notion of a semitone, one can now specify other intervals that are used in Western music theory. The naming conventions for these intervals are based on historical practice. In particular, an interval name may not only describe the difference in semitones between the lower and upper notes, but also how the interval is specified in score notation. Different note symbols may refer to the same note, which is known as enharmonic equivalence. Similarly, there exists enharmonic equivalence between musically different intervals (referred to by different interval names) that correspond to the same distance when measured in semitones (assuming the equal-tempered scale). For example, the two intervals named "augmented unison" and "minor second" both express the difference of one semitone, while specified differently when using score notation. In the following, even though being an oversimplification, we think of an interval in terms of a distance between pitches (given in semitones) while disregarding their music notation. The following figure shows the most common interval names (using the note C4 as reference of the lower note) and their meaning in terms of semitone differences (indicated by $\Delta$).
Frequency Ratios¶
The concept of intervals can be approached from a physical point of view by considering frequency relations that naturally occur between the harmonic partials of a pitched sound. Recall that the harmonics are the integer multiples of a fundamental frequency forming the harmonic series of a tone. In the physical approach, one derives the intervals from frequency relations between partials that occur within the same harmonic series. This is illustrated by the following figure, which shows the harmonic series of the note C2.
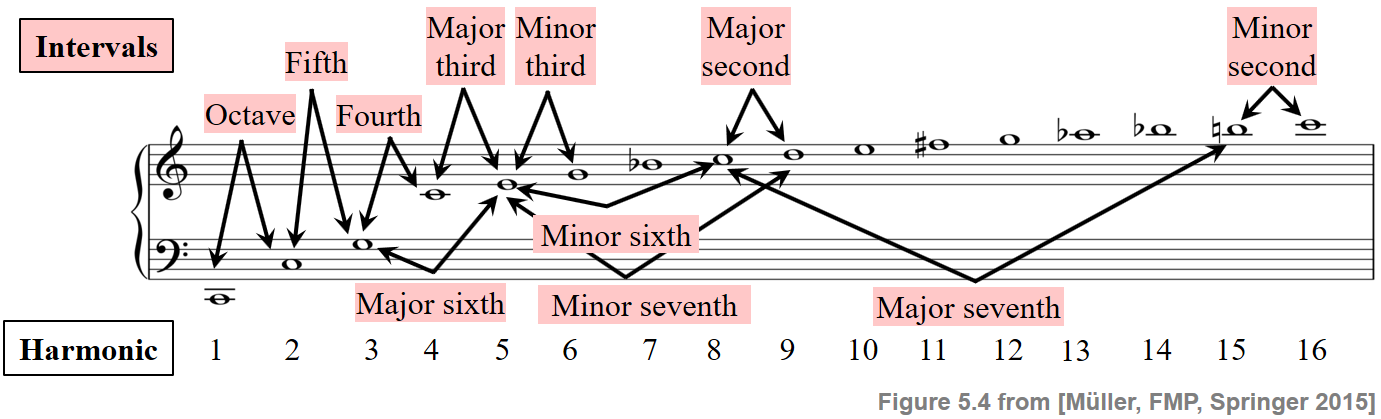
For example, the octave occurs as an interval between the first two partials, the fifth as an interval between the second and third partial, the fourth as an interval between the third and fourth partial, and so on. This observation leads to a definition of intervals that is based on ratios of small whole numbers. Any interval defined in this way is also called a pure or just interval. Similarly, the musical tuning based on harmonics is known as pure or just intonation.
Besides just intonation, there are many more tuning systems that may be used for defining intervals in terms of frequency ratios. The oldest known tuning system was introduced by the Greek philosopher and mathematician Pythagoras (sixth century BC). The geometrically motivated Pythagorean tuning is based only on the frequency ratio $1:2$ of the octave and the ratio $2:3$ of the fifth. All other intervals are derived from these ratios by suitably adding and subtracting fifths and octaves. This results in intervals that can be expressed by frequency ratios that involve only powers of two or powers of three.
In the following figure, we illustrate various definitions of intervals and their relations. The columns from left to right indicate the difference given in semitones ($\Delta$), the name of the interval, the interval assuming C4 as the root note, as well as the ratios with respect to just intonation (JI), and the Pythagorean ratios (Pyt).
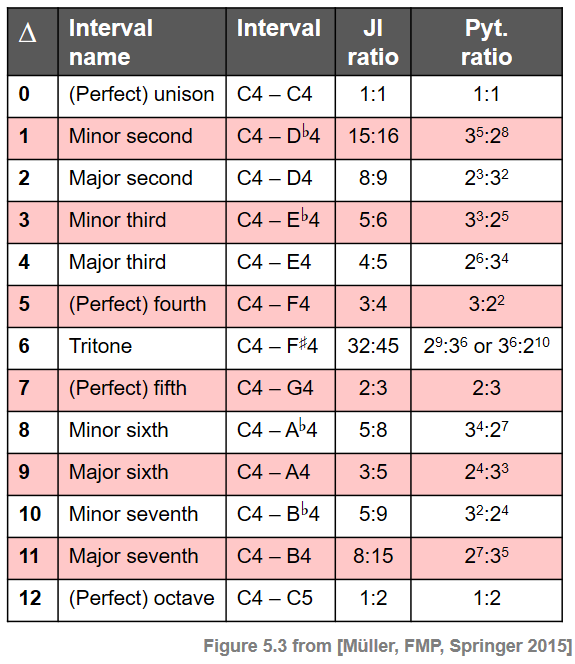
In the following code cell, we provide a sinusoidal sonification of the various intervals with respect to equal temperament (ET), just intonation (JI), and Pythagorean tuning (Pyt). Furthermore, we specify the deviations (given in cents) between the ET-based and JI-based intervals (JI Dev) as well as between the ET-based and Pyt-based intervals (Pyt Dev).
from collections import OrderedDict
import numpy as np
import IPython.display as ipd
import pandas as pd
def f_pitch(p):
frequency = 2 ** ((p - 69) / 12) * 440
return frequency
diff_semitones = ['0','1','2','3','4','5','6','7','8','9','10','11','12',]
JI_frac = ['$1:1$', '$15:16$', '$8:9$', '$5:6$', '$4:5$', '$3:4$', '$32:45$',
'$2:3$', '$5:8$', '$3:5$', '$5:9$', '$8:15$', '$1:2$']
JI_ratio = np.asarray([1, 15/16, 8/9, 5/6, 4/5, 3/4, 32/45, 2/3, 5/8, 3/5, 5/9, 8/15, 1/2])
pyt_frac = ['$1:1$', '$3^5:2^8$', '$2^3:3^2$', '$3^3:2^5$', '$2^6:3^4$', '$3:2^2$', '$2^9:3^6$',
'$2:3$', '$3^4:2^7$', '$2^4:3^3$', '$3^2:2^4$', '$2^7:3^5$', '$1:2$']
pyt_ratio = np.asarray([1, 243/256, 8/9, 27/32, 64/81, 3/4, 512/729, 2/3, 81/128, 16/27, 9/16, 128/243, 1/2])
p = 60
omega = f_pitch(p)
freq_JI = omega / JI_ratio
freq_pyt = omega / pyt_ratio
notes = np.asarray(range(p, p + 13))
freq_center = f_pitch(notes)
freq_deviation_cents_JI = np.log2(freq_JI / freq_center) * 1200
freq_deviation_cents_pyt = np.log2(freq_pyt / freq_center) * 1200
duration = 1
Fs = 4000
N = int(duration * Fs)
t = np.arange(0, N) / Fs
def generate_sinusoid(omega, t):
return np.sin(2 * np.pi * omega * t)
def generate_sinusoid_list(freq_list, x_ref=[]):
sinusoid_list = []
for f in freq_list:
s = generate_sinusoid(f, t)
x = np.concatenate((x_ref, s))
sinusoid_list.append(x)
return sinusoid_list
x_ref = generate_sinusoid(omega, t)
sinusoid_center = generate_sinusoid_list(freq_center, x_ref)
sinusoid_JI = generate_sinusoid_list(freq_JI, x_ref)
sinusoid_pyt = generate_sinusoid_list(freq_pyt, x_ref)
# Generation of html table
def generate_audio_tag_html_list(sinusoid_list, Fs):
audio_tag_html_list = []
for i in range(len(sinusoid_list)):
audio_tag = ipd.Audio( sinusoid_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 110px; height: 30px;"')
audio_tag_html_list.append(audio_tag_html)
return audio_tag_html_list
audio_tag_html_center = generate_audio_tag_html_list(sinusoid_center, Fs=Fs)
audio_tag_html_JI = generate_audio_tag_html_list(sinusoid_JI, Fs=Fs)
audio_tag_html_pyt = generate_audio_tag_html_list(sinusoid_pyt, Fs=Fs)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('$\Delta$', diff_semitones),
('Interval name', ['(Perfect) unison','Minor second','Major second','Minor Third',
'Major Third','(Perfect) fourth', 'Tritone','(Perfect) fifth',
'Minor sixth','Major sixth','Minor seventh','Major seventh','(Perfect) octave']),
(' Interval', ['C4–C4','C4–C$^\sharp$4','C4–D4',
'C4–D$^\sharp$4','C4–E4','C4–F4',
'C4–F$^\sharp$4','C4–G4','C4–G$^\sharp$4',
'C4–A4','C4–A$^\sharp$4', 'C4–B4','C4–C4']),
('ET Sinusoid', audio_tag_html_center),
('   JI Ratio', JI_frac),
('JI Sinusoid', audio_tag_html_JI),
('JI Dev', freq_deviation_cents_JI),
('   Pyt Ratio', pyt_frac),
('Pyt Sinusoid', audio_tag_html_pyt),
('Pyt Dev', freq_deviation_cents_pyt)]))
df.index = np.arange(1, len(df) + 1)
ipd.HTML(df.to_html(escape=False, index=False))
Consonance and Dissonance¶
Using the just intonation based on harmonic partials, we have seen that certain intervals can be described by ratios of small integers such as $1:1$ (unison), $1:2$ (octave), $2:3$ (fifth), or $3:4$ (fourth). Such intervals, which appear in the lower part of the harmonic series in a natural way, are usually perceived as coherent and pleasant. Used more generally, the term consonance refers to a combination of notes that sound pleasant to most people when being played simultaneously. In contrast, the term dissonance is used to refer to a combination of notes that sound harsh or unpleasant. Consonant sounds are considered to be stable (being at rest), as opposed to dissonant sounds that are considered to be unstable (having a transitional character).
There are various definitions of consonance and dissonance based on musical, physical, and perceptual criteria. As for intervals, the unisons, octaves, fifths, and fourths are usually considered to be in perfect consonance. Therefore, these intervals are sometimes also called the perfect intervals. The major and minor thirds, as well as major and minor sixths, are still perceived as somehow consonant (imperfect consonance)—however, to a lower degree. The other intervals are typically considered as dissonant. This particularly holds for the tritone interval, the most dissonant interval. As shown in the last section, the frequency ratio of the tritone in just intonation involves the largest integers. When playing notes simultaneously, the degree of consonance relates to how many of the harmonics of the played notes coincide. From this perspective, consonance does not only depend on the size of the interval between two notes, but also on the combined spectral distribution of the resulting sound. In the following code example, simultaneous intervals (also denoted as harmonic intervals) are generated with sinusoids according to different intonation schemes.
duration = 3
Fs = 4000
N = int(duration * Fs)
t = np.arange(0, N) / Fs
def generate_sinusoid_interval_list(freq_list, x_ref=[]):
sinusoid_list = []
for f in freq_list:
s = generate_sinusoid(f, t)
x = x_ref + s
sinusoid_list.append(x)
return sinusoid_list
x_ref = generate_sinusoid(omega, t)
sinusoid_center = generate_sinusoid_interval_list(freq_center, x_ref)
sinusoid_JI = generate_sinusoid_interval_list(freq_JI, x_ref)
sinusoid_pyt = generate_sinusoid_interval_list(freq_pyt, x_ref)
sinusoid_sum = list(range(len(freq_center)))
for i in range(len(freq_center)):
sinusoid_sum[i] = (sinusoid_center[i] + sinusoid_JI[i] + sinusoid_pyt[i]) / 3
# Generation of html table
def generate_audio_tag_html_list(sinusoid_freq_list, Fs):
audio_tag_html_list = []
for i in range(len(sinusoid_freq_list)):
audio_tag = ipd.Audio( sinusoid_freq_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 110px; height: 30px;"')
audio_tag_html_list.append(audio_tag_html)
return audio_tag_html_list
audio_tag_html_center = generate_audio_tag_html_list(sinusoid_center, Fs=Fs)
audio_tag_html_JI = generate_audio_tag_html_list(sinusoid_JI, Fs=Fs)
audio_tag_html_pyt = generate_audio_tag_html_list(sinusoid_pyt, Fs=Fs)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('Delta', diff_semitones),
('Interval name', ['(Perfect) unison','Minor second','Major second','Minor Third',
'Major Third','(Perfect) fourth', 'Tritone','(Perfect) fifth',
'Minor sixth','Major sixth','Minor seventh','Major seventh','(Perfect) octave']),
(' Interval', ['C4–C4','C4–C$^\sharp$4','C4–D4',
'C4–D$^\sharp$4','C4–E4','C4–F4',
'C4–F$^\sharp$4','C4–G4','C4–G$^\sharp$4',
'C4–A4','C4–A$^\sharp$4', 'C4–B4','C4–C4']),
('ET Sinusoid', audio_tag_html_center),
('   JI Ratio ', JI_frac),
('JI Sinusoid', audio_tag_html_JI),
('JI Dev.', freq_deviation_cents_JI),
('   Pyt Ratio ', pyt_frac),
('Pyt Sinusoid', audio_tag_html_pyt),
('Pyt Dev.', freq_deviation_cents_pyt)]))
df.index = np.arange(1, len(df) + 1)
ipd.HTML(df.to_html(escape=False, justify='center', index=False))










