Musical Notes and Pitches

Following Section 1.1.1 of [Müller, FMP, Springer 2015], we introduce in this notebook the notions of musical notes, pitches, and the twelve-tone equal-tempered scale.

Notes and Pitches

In music, the term note is often used in a rather loose way and may refer to both a musical symbol (when talking about score representations) as well as a pitched sound (when talking about audio representations). When thought of a musical symbol, each note has several attributes that determine the relative duration and the pitch of a sound to be performed by a musician. The notion of pitch is not strict and refers to a perceptual property that allows a listener to order a sound on a frequency-related scale. As discussed in Section 1.3 of [Müller, FMP, Springer 2015], playing a note on an instrument results in a (more or less) periodic sound of a certain fundamental frequency. This fundamental frequency is closely related to what is meant by the pitch of a note. The term "pitch" allows us to order pitched sounds from "lower" to "higher"—similarly to the keys of a piano keyboard ordered from left to right.

Pitch Class and Octaves

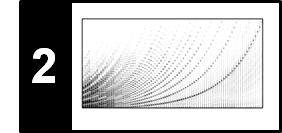
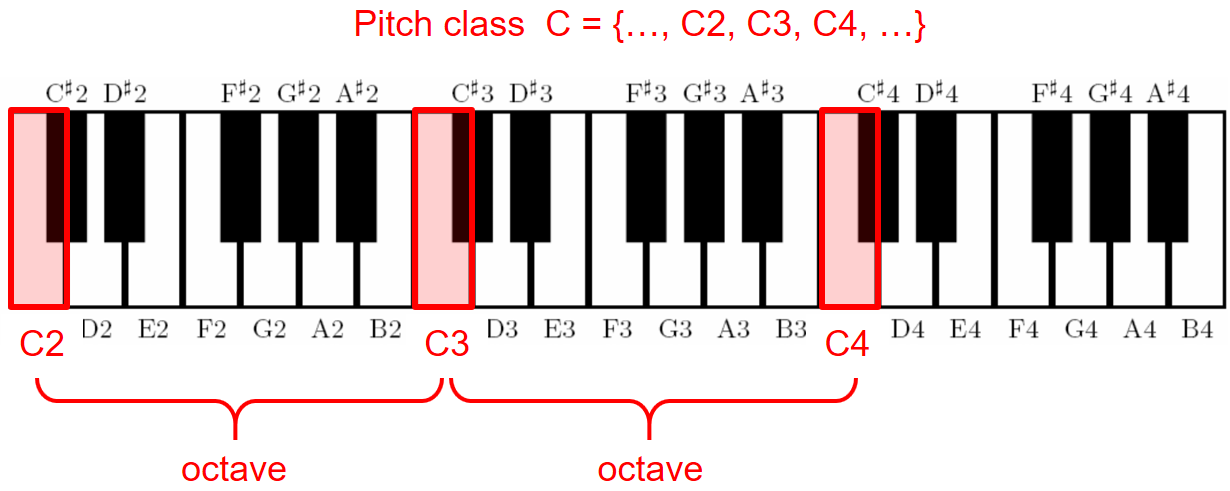
Two notes with fundamental frequencies in a ratio equal to any power of two (e.g., half, twice, or four times) are perceived as very similar. Because of that, all notes with this kind of relation can be grouped under the same pitch class. This observation also leads to the fundamental notion of an octave, which is defined to be the interval between one musical note and another one with half or double its fundamental frequency. Using this definition, a pitch class is a set of all pitches or notes that are an integer number of octaves apart. The following figure and sound example illustrates these concepts for the pitch class $\mathrm{C}$:

import numpy as np
import IPython.display as ipd

def generate_sinusoid_pitches(pitches=[69], dur=0.5, Fs=4000, amp=1):
    """Generation of sinusoids for a given list of MIDI pitches

    Notebook: C1/C1S1_MusicalNotesPitches.ipynb

    Args:
        pitches (list): List of MIDI pitches (Default value = [69])
        dur (float): Duration (in seconds) of each sinusoid (Default value = 0.5)
        Fs (scalar): Sampling rate (Default value = 4000)
        amp (float): Amplitude of generated signal (Default value = 1)

    Returns:
        x (np.ndarray): Signal
        t (np.ndarray): Time axis (in seconds)
    """
    N = int(dur * Fs)
    t = np.arange(N) / Fs
    x = []
    for p in pitches:
        freq = 2 ** ((p - 69) / 12) * 440
        x = np.append(x, np.sin(2 * np.pi * freq * t))
    x = amp * x / np.max(x)
    return x, t

dur = 1
Fs = 22050

pitches = [36,48,60,72,84,96,108]
x, t = generate_sinusoid_pitches(pitches=pitches, dur=dur, Fs=Fs, amp=0.5)
print('Pitch class C = {..., C1, C2, C3, C4, C5, C6, C7, ...}', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))

Pitch class C = {..., C1, C2, C3, C4, C5, C6, C7, ...}

Musical Scales

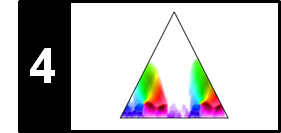
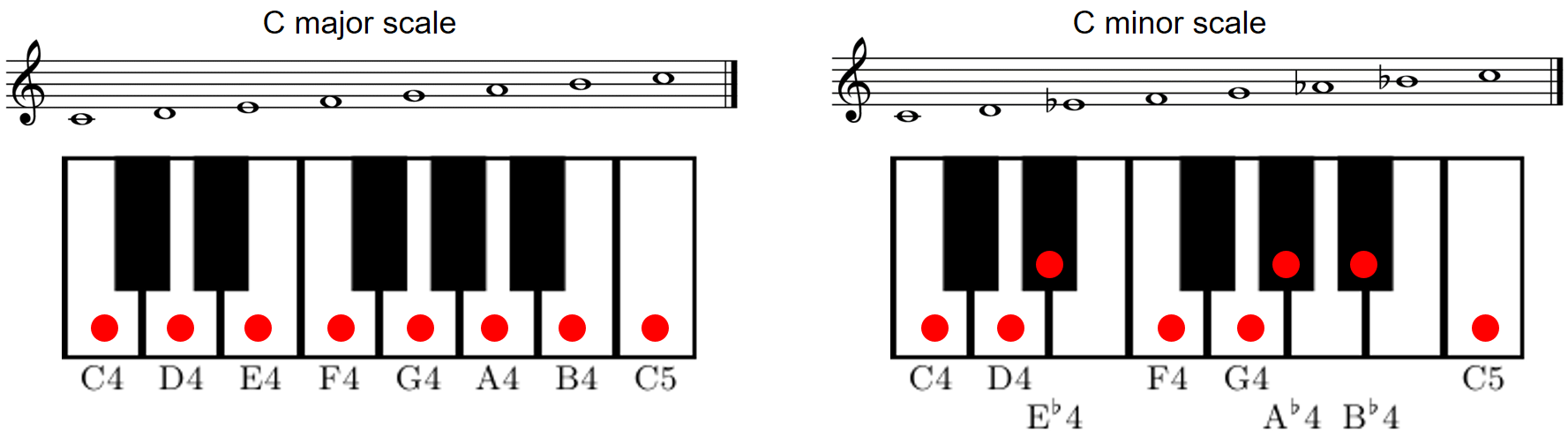
In order to describe music using a finite number of symbols, one needs to discretize the space of all possible pitches. This leads to the notion of a musical scale, which can be thought of as a finite set of representative pitches. Because of the close octave relationship of pitches, scales are generally considered to span a single octave, with higher or lower octaves simply repeating the pattern. A musical scale can then be specified by a division of the octave space into a certain number of scale steps. The elements of a scale are often simply referred to as the notes of the scale and are ordered according to their respective pitches. The following figure illustrates the case of a C major scale and a (natural) C minor scale.

dur = 0.5
Fs = 22050

x_maj, t = generate_sinusoid_pitches(pitches=[60,62,64,65,67,69,71,72], dur=dur, Fs=Fs, amp=0.5)
x_min, t = generate_sinusoid_pitches(pitches=[60,62,63,65,67,68,70,72], dur=dur, Fs=Fs, amp=0.5)

print('C major scale', flush=True)
ipd.display(ipd.Audio(data=x_maj, rate=Fs))
print('C minor scale', flush=True)
ipd.display(ipd.Audio(data=x_min, rate=Fs))

C major scale

C minor scale

Twelve-Tone Equal-Tempered Scale

In music history, many different scales have been suggested and used, and there have been fierce discussions about the suitability of specific scales. There is no universally valid musical scale, and the choice of a musical scale necessarily goes along with simplifications typically imposed by practical considerations. In the following, we consider the case of the twelve-tone equal-tempered scale, where an octave is subdivided into twelve scale steps. The fundamental frequencies of these steps are equally spaced on a logarithmic frequency axis (see Section 1.3.2 of [Müller, FMP, Springer 2015] and the notebook on Center Frequencies for MIDI note numbers). The difference between the fundamental frequencies of two subsequent scale steps is also called a semitone, which is the smallest possible interval in this scale.

Enharmonic Equivalence

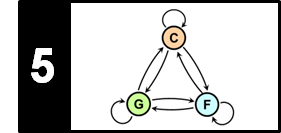
In the twelve-tone equal-tempered scale, there are twelve pitch classes. In Western music notation, these pitch classes are denoted by combining a letter-name and accidentals. Seven of the pitch classes (corresponding to C major) are denoted by the letters C, D, E, F, G, A, and B. These pitch classes correspond to the white keys of a piano keyboard. The remaining five pitch classes correspond to the black keys of a piano keyboard and are denoted by a combination of a letter and an accidental ($\sharp$, $\flat$). A sharp ($\sharp$) raises a note by a semitone, and a flat ($\flat$) lowers it by a semitone. The accidentals are written after the note name. For example, D$^\sharp$ represents D-sharp and D$^\flat$ represents D-flat. In the equal-tempered scale, the remaining five pitches can be either denoted by C$^\sharp$, D$^\sharp$, F$^\sharp$, G$^\sharp$, A$^\sharp$ or by D$^\flat$, E$^\flat$, G$^\flat$, A$^\flat$, B$^\flat$. For example, C$^\sharp$ and D$^\flat$ represent the same pitch class. This phenomenon is also known as enharmonic equivalence even though from a musical point of view one distinguishes between these two concepts.

Scientific Pitch Notation

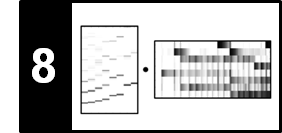
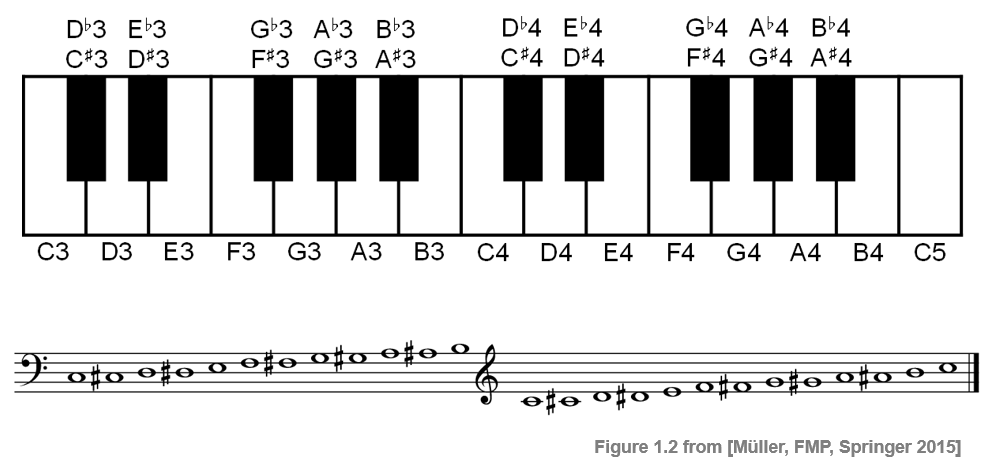
To name the notes of the twelve-tone equal-tempered scale, in addition to indicating the pitch class, one needs to provide an identifier for the octave. Following the Scientific Pitch Notation, each note is specified by the pitch class name, followed by a number that indicates the octave. The note A4 is determined to have a fundamental frequency of 440 Hz and serves as a reference. The octave number increases by one upon an ascension from a note with pitch class B to one with pitch class $\mathrm{C}$. The following figure shows a section of piano keyboard with keys ranging from C3 to C5 as well as corresponding notes using Western music notation.

Real piano recording of the chromatic scale ranging from C3 (p=48) to C5 (p=72):

dur = 0.25
Fs = 22050
pitches = range(48,73)

x_chromatic, t = generate_sinusoid_pitches(pitches=pitches, dur=dur, Fs=Fs, amp=0.5)

print('Sinusoidal sonification of the chromatic scale ranging from C3 (p=48) to C5 (p=72):', flush=True)
ipd.display(ipd.Audio(data=x_chromatic, rate=Fs))

Sinusoidal sonification of the chromatic scale ranging from C3 (p=48) to C5 (p=72):

Acknowledgment: This notebook was created by Meinard Müller.